Accueil > Enseignement > Cours gratuits > Optimisation et algorithmes génétiques > L’optimisation
L’optimisation
vendredi 7 juillet 2006, par
Parmi les problèmes rencontrés par le chercheur et l’ingénieur, les problèmes d’optimisation occupent à notre époque une place de choix. Nous n’aborderons pas le problème de l’optimisation d’un point de vue mathématique, mais simplement du point de vue d’un ingénieur pragmatique. Cette partie du cours ne sera donc pas exhaustive.
Le terme dispositif , que nous emploierons tout au long de ce cours, désignera l’objet, matériel ou non, que nous voulons étudier et optimiser : une molécule, un composant électronique, un process industriel, un système complexe, un programme informatique, etc.
Essai et erreur
La méthode de base pour optimiser un dispositif est la méthode d’ essai et erreur : il s’agit de tester un certain nombre de solutions potentielles jusqu’à l’obtention d’une solution adéquate. C’est ce que nous faisons quand nous donnons à un paramètres plusieurs valeurs successives et que nous observons le résultat. C’est également le cas quand nous faisons varier ce paramètre de façon quasi-continue à l’aide d’un ordinateur et que nous traçons la courbe correspondante.
- Figure 0
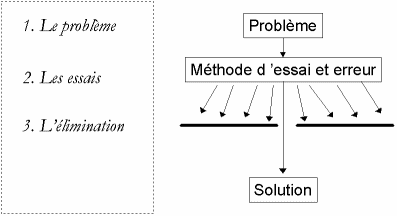
- On peut décrire l’apprentissage par essai et erreur par un schéma à trois niveaux [K. Popper, 1994].
Considérons la figure 0. Soit un problème : une situation nouvelle se présente et nécessite une solution qui n’est a priori pas connue. La méthode d’essai et erreur est alors employée : un grand nombre de solutions potentielles sont mises à l’essai. Les solutions inadéquates sont éliminées, jusqu’à ce qu’un essai se révèle satisfaisant. Ce schéma est très général. On peut l’appliquer au comportement des organismes vivant, à l’évolution des espèces (nous y reviendrons plus loin), à l’évolution des sciences ou au processus d’optimisation : " dans le fond, ce procédé semble être le seul qui soit logiquement possible. " [Popper, 1994] Les algorithmes informatiques constituent un puissant outil pour l’automatisation de ce processus.
- Figure 1
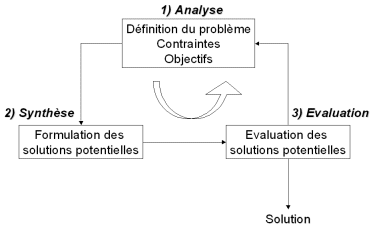
- Processus d’optimisation selon Asimow [Balachandran, 1993].
La figure 1 présente le processus d’optimisation en trois étapes : analyse, synthèse et évaluation [Balachandran, 1993]. Tout d’abord, il convient d’analyser le problème et d’opérer un certain nombre de choix préalables :
![]() Variables du problème. Quels sont les paramètres intéressants à faire varier ?
Variables du problème. Quels sont les paramètres intéressants à faire varier ?
![]() Espace de recherche. Dans quelles limites faire varier ces paramètres ?
Espace de recherche. Dans quelles limites faire varier ces paramètres ?
![]() Fonctions objectif. Quels sont les objectifs à atteindre ? Comment les exprimer mathématiquement ?
Fonctions objectif. Quels sont les objectifs à atteindre ? Comment les exprimer mathématiquement ?
![]() Méthode d’optimisation. Quelle méthode choisir ?
Méthode d’optimisation. Quelle méthode choisir ?
Après cette phase d’anlyse, la méthode choisie synthétise des solutions potentielles qui sont évaluées, puis éventuellement éliminées jusqu’à obtention d’une solution acceptable. Si nécessaire, le problème peut être alors redéfini à partir des solutions déjà obtenues.
Variables du problème
C’est à l’utilisateur de définir les variables du problème. Il peut avoir intérêt à faire varier un grand nombre de paramètres pour augmenter les degrés de liberté de l’algorithme afin de découvrir des solutions nouvelles. Ou bien, s’il a une vue suffisamment précise de ce qu’il veut obtenir, il peut limiter le nombre de variables à l’essentiel.
Les variables peuvent être de natures diverses. Par exemple, pour un composant électronique il peut s’agir de sa forme et de ses dimensions géométriques, des matériaux utilisés, des conditions de polarisation, etc. Nous désignerons par x1,…,xn les n variables du problème. Celles-ci peuvent être réelles, complexes, entières, booléennes, etc. Dans la suite du cours nous les supposerons réelles.
Espace de recherche
Dans certains algorithmes d’optimisation, tels que les stratégies d’évolution , l’espace de recherche est infini : seule la population initiale est confinée dans un espace fini [Bäck, 1991]. Mais dans le cas des algorithmes de type Monte Carlo et génétique , il est généralement nécessaire de définir un espace de recherche fini. Cette limitation de l’espace de recherche n’est généralement pas problématique. En effet, ne serait-ce que pour des raisons technologiques ou informatiques (taille de la fenêtre de modélisation), les intervalles de définition des variables sont en général naturellement limités. De plus, on a souvent une idée des ordres de grandeur des variables du problème.
Nous désignerons par ximin et ximax les bornes de chaque variable xi :
![]()
Fonctions objectif et fonction d’adaptation
La ou les grandeurs à optimiser peuvent être par exemple une consommation, un rendement, un facteur de transmission, un profit, la faisabilité technologique, un coût, une durée de développement, etc. Un algorithme d’optimisation nécessite généralement la définition d’une fonction rendant compte de la pertinence des solutions potentielles, à partir des grandeurs à optimiser. Nous la nommerons fonction d’adaptation f (ou fitness function en terminologie anglo-saxonne). L’algorithme convergera vers un optimum de cette fonction, quelle que soit sa définition. La pertinence de la solution dépendra donc de la pertinence de la " question " posée à l’ordinateur. La fonction f doit donc exprimer le plus fidèlement possible le désir de l’utilisateur sous forme mathématique. C’est une fonction des variables x1,…,xn . Sa définition peut être simplement analytique, ou elle peut faire appel à un modèle numérique du dispositif étudié, ou elle peut éventuellement faire appel au jugement de l’utilisateur, etc.
Objectif unique
Dans le cas d’un objectif unique , la définition de f ne pose généralement pas de problème. Par exemple, si l’on se fixe l’objectif de trouver un dispositif dont le rendement est maximum, f sera égale au rendement. Dans le cas où l’on utilise un modèle numérique, on commence par évaluer les caractéristiques des solutions potentielles en utilisant le modèle. Puis on calcule la fonction d’adaptation à partir de ces caractéristiques.
Dans ce cours, nous utiliserons des fonctions d’adaptation normalisées sur l’intervalle [0 ; 1]. La valeur 0 correspondra à une solution totalement inadaptée et la valeur 1 à une solution parfaite.
Objectifs multiples
Certains problèmes d’optimisation doivent satisfaire des objectifs multiples , souvent concurrents, ce qui implique un compromis. La méthode classique consiste à définir plusieurs fonctions objectif f i , traduisant chaque objectif à atteindre, et à les combiner au sein de la fonction d’adaptation. La combinaison la plus simple est une somme pondérée des fonctions objectif [Fonseca, 1993] :
![]()
où les poids  i doivent être tels que la fonction d’adaptation reste bornée dans l’intervalle [0 ; 1]. (1)
i doivent être tels que la fonction d’adaptation reste bornée dans l’intervalle [0 ; 1]. (1)
Remarquons qu’un poids peut être négatif afin de tenir compte de certaines contraintes du problème.
C’est à l’utilisateur de fixer convenablement les poids. On peut généralement classer les objectifs par importance mais les poids devront souvent être adaptés par tâtonnement. Le processus d’optimisation a beau être automatisé, l’utilisateur doit donc quand même optimiser " à la main " la définition de la fonction d’adaptation. Dans la littérature, ce problème délicat est souvent laissé dans l’ombre.
A la place d’une somme, on peut également utiliser un produit du type :
![]() (2)
(2)
ou des expressions plus complexes telle qu’une combinaison de sommes et de produits.
Il faut néanmoins être conscient des effets d’une combinaison des objectifs. Deux solutions potentielles dont les fonctions objectif n’ont pas les mêmes valeurs peuvent mener à une même valeur de la fonction d’adaptation ! De plus, un algorithme utilisant une telle approche ne convergera à chaque fois que vers une seule solution alors qu’il existe peut-être toute une famille de solutions. Cette famille correspond alors à un sous-ensemble de l’espace de recherche, que l’on peut par exemple se réprésenter sous forme d’une nappe dans un espace à trois dimensions.
L’optimisation à objectifs multiples est un domaine de recherche très actif car les enjeux économiques et industriels sont énormes. Des concepts tels que les niches écologiques ou l’optimalité de Pareto semblent prometteurs [Fonseca, 1995].
Méthodes d’optimisation
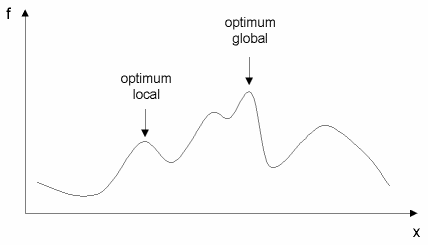
Une fois définie la fonction à optimiser, il s’agit de choisir une méthode adaptée au problème posé. Les méthodes d’optimisation peuvent être classées de différentes manières : nous les classerons en méthodes déterministes et méthodes non-déterministes. Les méthodes déterministes sont généralement efficaces quand l’évaluation de la fonction est très rapide, ou quand la forme de la fonction est connue a priori . Les cas plus complexes (temps de calcul important, nombreux optima locaux, fonctions non-dérivables, fonctions fractales, fonctions bruitées…) seront souvent traités plus efficacement par des méthodes non-déterministes.
Méthodes déterministes
La recherche des extrema d’une fonction f revient à résoudre un système de n équations à n inconnues, linéaire ou non :
![]() (3)
(3)
On peut donc utiliser des méthodes classiques telles que la méthode du gradient ou la méthode de Gauss-Seidel [Ciarlet, 1990 et Nougier, 1987]. En général, l’utilisation de ces méthodes nécessite comme étape préliminaire la localisation des extrema. Celle-ci peut être faite, par exemple, sur un graphique ou par une discrétisation fine de l’espace de recherche. La fonction à optimiser est évaluée en chacun des points de discrétisation. La valeur maximale est alors considérée comme une bonne approximation de l’optimum de la fonction. Cette méthode est brutale et le temps de calcul augmentera exponentiellement en fonction du nombre de variables.
En effet, considérons une optimisation sur huit variables. Si on discrétise l’intervalle de définition de chaque variable en seulement 3 points, une exploration systématique nécessite 38 = 6561 exécutions du modèle. Dans le cas d’un modèle physique nécessitant 10 secondes de calcul sur un PC standard, cela représente 18 heures de calcul, pour un résultat inutilisable !
Méthodes non-déterministes
Ces méthodes font appel à des tirages de nombres aléatoires. Elles permettent d’explorer l’espace de recherche plus efficacement. Citons entre autres [Beasley, 1993a] :
![]() Les méthodes Monte Carlo : la fonction est évaluée en un grand nombre de points choisis aléatoirement.
Les méthodes Monte Carlo : la fonction est évaluée en un grand nombre de points choisis aléatoirement.
![]() Les méthodes hybrides : on peut par exemple utiliser la méthode des gradients en partant d’un grand nombre de points choisis aléatoirement. On peut ainsi espérer déterminer au fur et à mesure tous les optima locaux de la fonction.
Les méthodes hybrides : on peut par exemple utiliser la méthode des gradients en partant d’un grand nombre de points choisis aléatoirement. On peut ainsi espérer déterminer au fur et à mesure tous les optima locaux de la fonction.
![]() Le recuit simulé : on effectue des déplacements aléatoires à partir d’un point initial. Si un déplacement mène à une valeur plus grande de la fonction f , il est accepté. Sinon, il est accepté avec une probabilité :
Le recuit simulé : on effectue des déplacements aléatoires à partir d’un point initial. Si un déplacement mène à une valeur plus grande de la fonction f , il est accepté. Sinon, il est accepté avec une probabilité :
![]() (4)
(4)
où "delta f" est la variation de la fonction, T est assimilé à une température qui décroît au cours du temps et k est une constante. Cette méthode est basée sur une analogie avec les processus de recuit utilisés en métallurgie et qui visent à atteindre une configuration d’énergie minimale ( -f est alors assimilée à une énergie).
![]() Les Algorithmes Evolutionnaires : le principe est de simuler l’évolution d’une population d’individus divers auxquels on applique différents opérateurs génétiques et que l’on soumet à chaque génération à une sélection. Ces algorithmes sont de plus en plus utilisés dans l’industrie car ils sont particulièrement adaptés aux problèmes d’optimisation comportant de nombreux paramètres.
Les Algorithmes Evolutionnaires : le principe est de simuler l’évolution d’une population d’individus divers auxquels on applique différents opérateurs génétiques et que l’on soumet à chaque génération à une sélection. Ces algorithmes sont de plus en plus utilisés dans l’industrie car ils sont particulièrement adaptés aux problèmes d’optimisation comportant de nombreux paramètres.
Compromis exploration et exploitation
Si nous opposons exploration et exploitation de l’espace de recherche, nous pouvons dire que les méthodes Monte Carlo permettent une bonne exploration puisque tout point a une probabilité identique d’être atteint, mais qu’il n’y a pas d’exploitation des résultats déjà obtenus. Avec la méthode des gradients, l’exploration est moindre mais l’exploitation des données précédentes par l’intermédiaire des gradients permet une bonne recherche locale. Enfin, les Algorithmes Evolutionnaires offrent un bon compromis entre exploration et exploitation [Beasley, 1993a]. Nous allons nous y intéresser de plus près.