Méthodes de l’AG

Codage des variables

La première étape est de définir et de coder convenablement le problème. A chaque variable d’optimisation xi (à chaque paramètre du dispositif), nous faisons correspondre un gène . Nous appelons chromosome un ensemble de gènes. Chaque dispositif est représenté par un individu doté d’un génotype constitué d’un ou plusieurs chromosomes. Nous appelons population un ensemble de N individus que nous allons faire évoluer.

D’un point de vue informatique, nous utilisons dans notre algorithme un codage binaire. C’est-à-dire qu’un gène est un entier long (32 bits). Un chromosome est un tableau de gènes (figure 4 et figure 5). Un individu est un tableau de chromosomes. La population est un tableau d’individus. Notons qu’on pourrait aussi utiliser d’autres formes de codage (réel, codage de Gray...) [Davis, 1991].

On aboutit à une structure présentant cinq niveaux d’organisation (figure 3), d’où résulte le comportement complexe des AG :

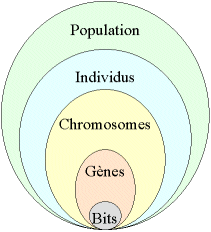
Figure 3

Les cinq niveaux d’organisation de notre Algorithme Génétique.

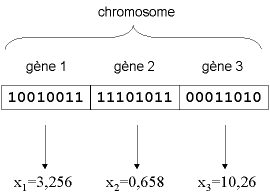
Figure 4 : illustration schématique du codage des variables d’optimisation xi .

Un des avantages du codage binaire est que l’on peut ainsi facilement coder toutes sortes d’objets : des réels, des entiers, des valeurs booléennes, des chaînes de caractères… Cela nécessite simplement l’usage de fonctions de codage et décodage pour passer d’une représentation à l’autre.

Rappelons que dans cette étude les n variables sont supposées réelles. Nous considérons un espace de recherche fini :

Afin de coder nos variables réelles en binaire, nous discrétisons l’espace de recherche. Ainsi un codage sur 32 bits implique une discrétisation des intervalles en gmax =232-1= 4 294 967 295 valeurs discrètes. Notons au passage que si cette discrétisation est plus fine que celle du modèle physique utilisé, la fonction est assimilable à une fonction escalier, si on la considère à une échelle suffisamment petite.

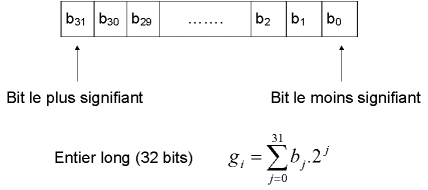
Figure 5 : chaque gène (chaque paramètre du dispositif) est codé par un entier long (32 bits).

A chaque variable réelle xi on associe donc un entier long gi  :

Les formules de codage et décodage sont alors les suivantes :

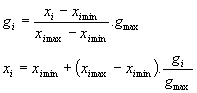(5)

Genèse de la population

La première étape de l’algorithme est la genèse de la population, c’est-à-dire le choix des dispositifs de départ que nous allons faire évoluer. On pourrait prendre des individus régulièrement répartis dans l’espace. Néanmoins, une initialisation aléatoire est plus simple à réaliser : les valeurs gi des gènes sont tirées au hasard selon une distribution uniforme. Notons qu’on peut, si nécessaire, introduire des individus déjà calculés.

Nous discuterons plus loin de la taille N de cette population, mais nous pouvons déjà dire qu’elle résultera d’un compromis entre temps de calcul et qualité de la solution.

Evaluation

L’évaluation de chaque dispositif est réalisée par le modèle utilisé. Si le dispositif possède plusieurs états de fonctionnement, le modèle peut être lancé plusieurs fois. Les résultats obtenus sont alors utilisés pour calculer les fonctions objectif et la fonction d’adaptation.

Notons que dans le cas d’un modèle physique, la majeure partie du temps de calcul sera probablement due à l’exécution de ce modèle. En effet, le reste de l’AG est essentiellement composé de manipulation d’entiers et de bits, donc très rapide.

Sélection – élimination

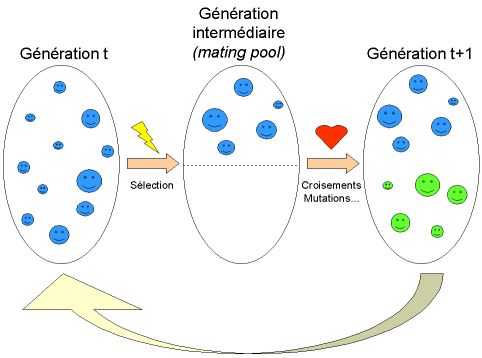
Figure 6 : représentation schématique du fonctionnement de notre algorithme.

Nous appelons génération la population à un instant t donné. Une fois réalisée l’évaluation de la génération, on opère une sélection à partir de la fonction d’adaptation. Seuls les individus passant l’épreuve de sélection (rappelons qu’il ne s’agit ici que de dispositifs !) peuvent accéder à la génération intermédiaire ( mating pool en terminologie anglo-saxonne) et s’y reproduire. En fait, cette génération intermédiaire est deux fois plus petite ( N/2 dispositifs) que la génération dont elle est issue (figure 6). Notre algorithme étant conçu de façon à ce que chaque couple d’individus parents donne naissance à deux enfants, nous aboutissons à nouveau à une génération entière à l’instant t+1.

Nous avons essayé deux techniques de sélection [Michalewicz, 1994] :
 " N /2-élitisme " : les individus sont triés selon leur fonction d’adaptation. Seule la moitié supérieure de la population, correspondant aux meilleurs composants, est sélectionnée. Nous avons pu constater que cette méthode induisait une convergence prématurée de l’algorithme : la pression de sélection est trop forte. Il est en effet nécessaire de maintenir une diversité génétique suffisante dans la population, celle-ci constituant un réservoir de gènes pouvant être utiles par la suite. En effet, tout individu peut transmettre à sa descendance des gènes (paramètres de composant) qui, une fois combinés avec d’autres, peuvent se révéler intéressants. Nous avons donc essayé la méthode suivante.
 " sélection par tournoi " : deux individus sont choisis au hasard et combattent (on compare leurs fonctions d’adaptation) pour accéder à la génération intermédiaire. Le plus adapté l’emporte avec une probabilité , que nous avons généralement prise égale à 1 (une valeur inférieure permet de réduire la pression de sélection si nécessaire). Cette étape est répétée jusqu’à ce que la génération intermédiaire soit remplie ( N /2 composants). Il est tout à fait possible que certains individus participent à plusieurs tournois : s’ils gagnent plusieurs fois, ils auront donc droit d’être copiés plusieurs fois dans la génération intermédiaire, ce qui favorisera la pérennité de leurs gènes.

Les résultats de ce chapitre ont été obtenus avec cette dernière méthode, à laquelle nous avons associé une procédure d’élitisme : si par hasard l’individu le plus adapté (le meilleur dispositif) n’a pas été sélectionné, il est copié d’office dans la génération intermédiaire à la place d’un individu choisi aléatoirement.

Opérateur croisement

Une fois la génération intermédiaire à moitié remplie, les individus sont aléatoirement répartis en couples hermaphrodites. Les chromosomes (ensembles de paramètres) des parents sont alors copiés et recombinés de façon à former deux descendants possédant des caractéristiques issues des deux parents. On forme ainsi la génération t +1 (Figure 6).

L’opérateur croisement favorise l’exploration de l’espace de recherche. Considérons deux gènes A et B pouvant être améliorés par mutation. Il est peu probable que les deux gènes améliorés A’ et B’ apparaissent par mutation dans un même individu. Mais l’opérateur de croisement permettra de combiner rapidement A’ et B’ dans la descendance de deux parents portant chacun un des gènes mutants. Il est alors possible que la présence simultanée des deux gènes produise un individu encore plus adapté [Dessales, 1996]. L’opérateur de croisement assure donc le brassage du matériel génétique et l’accumulation des mutations favorables. En termes plus concrets, cet opérateur permet de créer de nouvelles combinaisons des paramètres des composants.

Le phénomène de croisement est une propriété naturelle de l’ADN. C’est par analogie qu’ont été conçus les opérateurs de croisement dans les AG. Nous avons testé deux méthodes de croisement classiques :
- " croisement en un point " : on choisit au hasard un point de croisement, pour chaque couple (Figure 7). Notons que le croisement s’effectue directement au niveau binaire, et non pas au niveau des gènes. Un chromosome peut donc être coupé au milieu d’un gène.

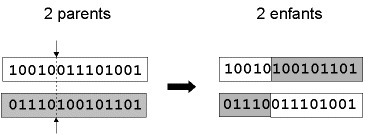
Figure 7 : représentation schématique du croisement en 1 point. Les chromosomes sont bien sûr généralement beaucoup plus longs.

 " croisement un deux points " : on choisit au hasard deux points de croisement (Figure 8). Par la suite, nous avons utilisé cet opérateur car il est généralement considéré comme plus efficace que le précédent [Beasley, 1993b]. Néanmoins nous n’avons pas constaté de différence notable dans la convergence de l’algorithme.

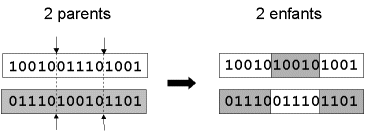
Figure 8 : représentation schématique du croisement en 2 points.

Notons que d’autres formes de croisement existent, du croisement en k points jusqu’au cas limite du croisement uniforme…

Opérateur mutation

Nous définissons une mutation comme étant l’inversion d’un bit dans un chromosome (Figure 9). Cela revient à modifier aléatoirement la valeur d’un paramètre du dispositif. Les mutations jouent le rôle de bruit et empêchent l’évolution de se figer. Elles permettent d’assurer une recherche aussi bien globale que locale, selon le poids et le nombre des bits mutés. De plus, elles garantissent mathématiquement que l’optimum global peut être atteint.

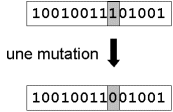
Figure 9 : représentation schématique d’une mutation dans un chromosome.

D’autre part, une population trop petite peut s’homogénéiser à cause des erreurs stochastiques : les gènes favorisés par le hasard peuvent se répandre au détriment des autres. Cet autre mécanisme de l’évolution, qui existe même en l’absence de sélection, est connu sous le nom de dérive génétique. Du point de vue du dispositif, cela signifie que l’on risque alors d’aboutir à des dispositifs qui ne seront pas forcément optimaux. Les mutations permettent de contrebalancer cet effet en introduisant constamment de nouveaux gènes dans la population [Beasley, 1993b].

Comment réaliser notre opérateur mutation ? De nombreuses méthodes existent. Souvent la probabilité de mutation pm par bit et par génération est fixée entre 0,001 et 0,01. On peut prendre également pm =1/l où l est le nombre de bits composant un chromosome. Il est possible d’associer une probabilité différente à chaque gène. Et ces probabilités peuvent être fixes ou évoluer dans le temps.

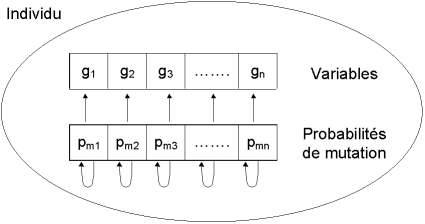
Figure 10 : principe de l’auto-adaptation. A chaque variable est associée sa propre probabilité de mutation, qui est elle-même soumise au processus d’évolution. L’individu possède donc un second chromosome codant ces probabilités.

Après divers essais, nous avons abouti à la méthode d’ auto-adaptation des probabilités de mutation [Bäck, 1992]. Si dans un environnement stable il est préférable d’avoir un taux de mutation faible, la survie d’une espèce dans un environnement subissant une évolution rapide nécessite un taux de mutation élevé permettant une adaptation rapide. Les taux de mutation d’une espèce dépendent donc de leur environnement [Wills, 1991].

Pour prendre en compte cette formulation biologique et l’adapter à notre cas, nous avons introduit dans chaque individu (dispositif) un second chromosome (ensemble de paramètres) dont les gènes (paramètres) représentent les probabilités de mutation de chaque gène du premier chromosome (Figure 10). Ce second chromosome est géré de façon identique au premier, c’est-à-dire qu’il est lui-même soumis aux opérateurs génétiques (croisement et mutation). Cela revient à fixer les probabilités assurant la modification des valeurs des paramètres du composant en fonction des valeurs d’un ensemble d’autres paramètres (les probabilités de mutation).

Lors de la genèse, les probabilités de mutation sont posées égales à 0,1 (valeur qui nous a paru la meilleure après plusieurs essais). Au cours du déroulement de l’algorithme, les gènes et les individus ayant des probabilités de mutation trop élevées ont tendance à disparaître. De même, les gènes ayant des probabilités de mutation trop faibles ne peuvent pas évoluer favorablement et tendent à être supplantés. Les probabilités de mutation dépendent donc du gène considéré et de la taille de la population. De plus, elles évoluent au cours du temps. Il y a donc auto-adaptation des probabilités de mutation.

Chapitre suivant