Accueil > Enseignement > Cours gratuits > Optimisation et algorithmes génétiques > Convergence de l’AG
Convergence de l’AG
vendredi 7 juillet 2006, par
Convergence et temps de calcul
On peut constater figure 11 que l’amélioration de la population est très rapide au début (recherche globale) et devient de plus en plus lente à mesure que le temps passe (recherche locale) . Le bruit dans la moyenne est essentiellement dû aux mutations.
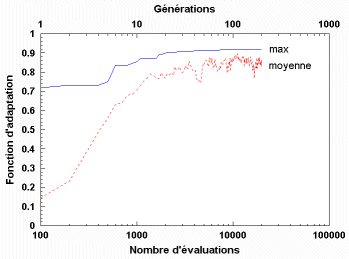
- Figure 11
- Exemple de convergence de l’AG. On a reporté la valeur de la fonction d’adaptation de l’individu le plus adapté de chaque génération (trait), et la moyenne des fonctions d’adaptation (pointillés), pour une population de 200 individus.
On voit que la valeur moyenne de la fonction d’adaptation a tendance à se rapprocher de celle de l’individu le plus adapté. Cela correspond à une uniformisation croissante de la population. Nous avons donc introduit dans notre logiciel une fenêtre graphique (Figure 12) permettant de visualiser la totalité de la population [Dessales, 1996]. Chaque ligne représente le génotype d’un individu, autrement dit les bits qui conduisent aux valeurs des paramètres d’un composant. Chaque pixel représente la valeur d’un bit dans son chromosome principal (blanc pour 0, et noir pour 1). Chaque groupe de 32 bits, entre deux graduations de la Figure 12, correspond à un gène. Les individus sont triés selon leur fonction d’adaptation : les plus adaptés correspondent aux lignes du haut, les moins adaptés aux dernières lignes. Dans cet exemple, nous avons représenté une population aux générations 1, 3, 10, 20, 50 et 130 (de gauche à droite, et de haut en bas). La taille de la population est de 200 individus (dispositifs) et le chromosome principal comprend 8 gènes (paramètres) de 32 bits.



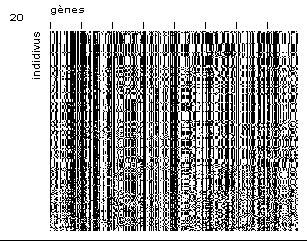
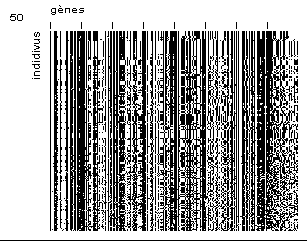
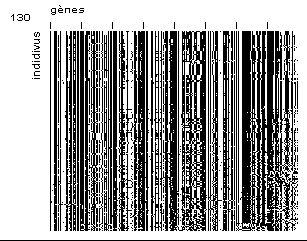
Figure 12 : générations 1, 3, 10, 20, 50 et 130. Chaque pixel représente un bit du chromosome principal d’un individu. Optimisation comportant 8 variables et 200 individus.
Ce genre de représentation permet de mieux comprendre le fonctionnement de l’algorithme. Tout d’abord la première image représente la population initiale tirée aléatoirement et ne présente donc aucun motif apparent. Les images suivantes (génération 3, 10 et 20) montrent l’apparition progressive de schémas, ce qui signifie que certaines valeurs des paramètres du composant se propagent dans la population parce qu’elles procurent un avantage aux individus qui en sont porteurs. Sur les deux dernières images (générations 50 et 130), on voit que la population s’est à peu près uniformisée. L’utilisateur peut alors stopper l’algorithme.
En chargeant le fichier suivant, vous pourrez voir le film entier : charger le film au format AVI (1,3 Mo !) (cliquez sur le bouton droit de votre souris pour télécharger le fichier)
Un des intérêts des AE et AG est que le temps de calcul ne croît pas exponentiellement avec le nombre n de variables, mais plutôt en n.ln(n). D’autre part, ce temps de calcul est proportionnel au temps de calcul de la fonction d’adaptation, donc du modèle utilisé, et à la taille de la population.
Réglage des paramètres de l’AG
Quelle doit être la taille de cette population ? Une population trop petite évoluera probablement vers un optimum local peu intéressant. Une population trop grande sera inutile car le temps de convergence sera excessif. La taille de la population doit être choisie de façon à réaliser un bon compromis entre temps de calcul et qualité du résultat.
Pour le problème qui nous intéressait et avec les moyens de calcul dont nous disposions, nous avons pu constater qu’une population de 100 individus constituait un bon compromis. Nous pouvions ainsi calculer 100 à 200 générations en une nuit sur un Pentium Pro 200 MHz.
Mais il faut être conscient que cette taille de population dépend de la puissance de calcul dont on dispose, des méthodes utilisées (sélection, opérateurs génétiques…), du nombre de variables considérées et de la fonction d’adaptation. Si la fonction à optimiser comporte peu d’optima locaux et un optimum global net, la population nécessaire sera plus petite que dans le cas d’une fonction beaucoup plus compliquée comportant de nombreux optima locaux.
Nous touchons là au délicat problème du réglage des paramètres de l’algorithme. Celui-ci doit être optimisé pour chaque type de problème traité, ce qui constitue une part importante du travail de l’utilisateur. Les caractéristiques de l’algorithme doivent être adaptées à la topologie du paysage dessiné par la fonction (fitness landscape) . L’ensemble problème-méthodes-paramètres constitue donc un tout. En témoigne certaines études où les paramètres d’un Algorithme Génétique sont réglés et optimisés par un autre Algorithme Génétique [Goldberg, 1994]. Dans la pratique, les méthodes et paramètres des AG sont tout d’abord réglés approximativement par tâtonnement avec des fonctions de n variables couramment utilisées pour tester les algorithmes d’optimisation. Le temps de calcul de ces fonctions étant minime, on peut ainsi régler rapidement les paramètres. Nous avons ainsi utilisé une fonction sphérique, une fonction de Fletcher-Powell et une fonction fractale [Bäck, 1996]. Nous avons ensuite réglé plus finement les paramètres en fonction des problèmes traités.